About me
I am a research engineer and former mathematician with a passion for translating advanced mathematical and computational methods into real-world applications. My professional background spans data science, machine learning research, and quantitative analysis.
I earned my PhD in Mathematics from the University of Waterloo in 2021, and I hold both a master’s and a bachelor’s degree in Mathematics from Sharif University of Technology. My PhD research focused on Stochastic Optimization, while my earlier studies delved into Fundamental Mathematics. You can find my CV here.
Notes
Projects
- Solving Pasur Using GPU-Accelerated Counterfactual Regret Minimization
- Generative Modeling of Heston Volatility Surfaces Using Variational Autoencoders
- Implementing Deep Smoothing for Implied Volatility Surfaces
- Quantitative Finance and Option Pricing
- A Termination Criterion for Stochastic Gradient Descent for Binary Classification
Solving Pasur Using GPU-Accelerated Counterfactual Regret Minimization
Pasur is a fishing card game played over six rounds and is played similarly to games such as Cassino and Scopa, and Bastra. This paper introduces a CUDA-accelerated computational framework for simulating Pasur, emphasizing efficient memory management. We use our framework to compute near-Nash equilibria via Counterfactual Regret Minimization (CFR), a well-known algorithm for solving large imperfect-information games. To see project’s page, click here. You can find the code for this project here.
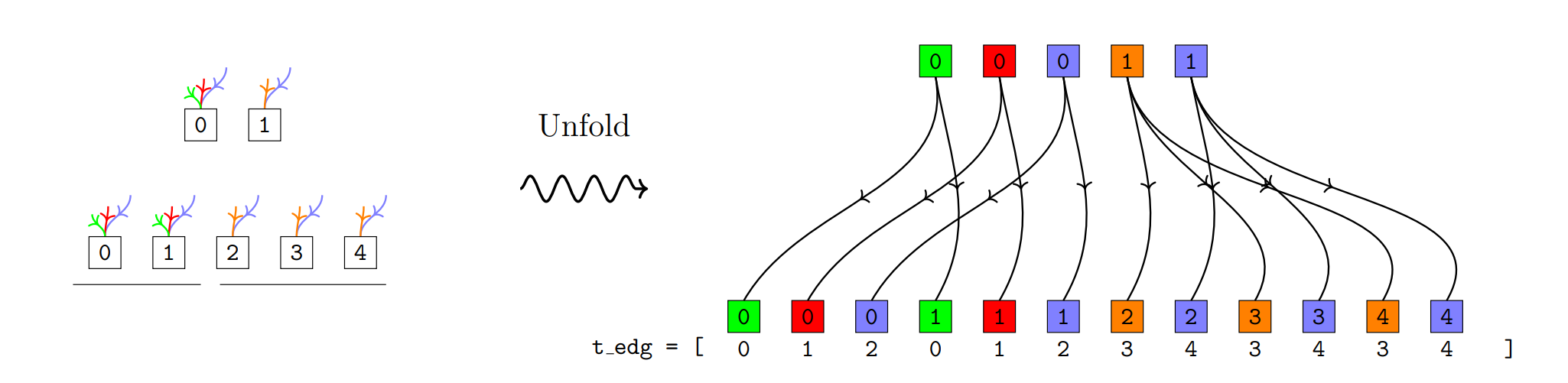
Tags: Counterfactual Regret Minimization, Reinforcement Learning, PyTorch, Nash Equilibrium, Game Theory, Memory Management, GPU Optimization, Efficient Computing, Artificial Intelligence
Generative Modeling of Heston Volatility Surfaces Using Variational Autoencoders
This project focuses on training a Variational Autoencoder (VAE) to produce Heston volatility surfaces. The Heston model is used in stochastic volatility option pricing models. Once trained, this VAE can generate new volatility surfaces, which could be useful for various financial applications such pricing exotic derivatives. To see project’s page, click here. You can find the code for this project here.
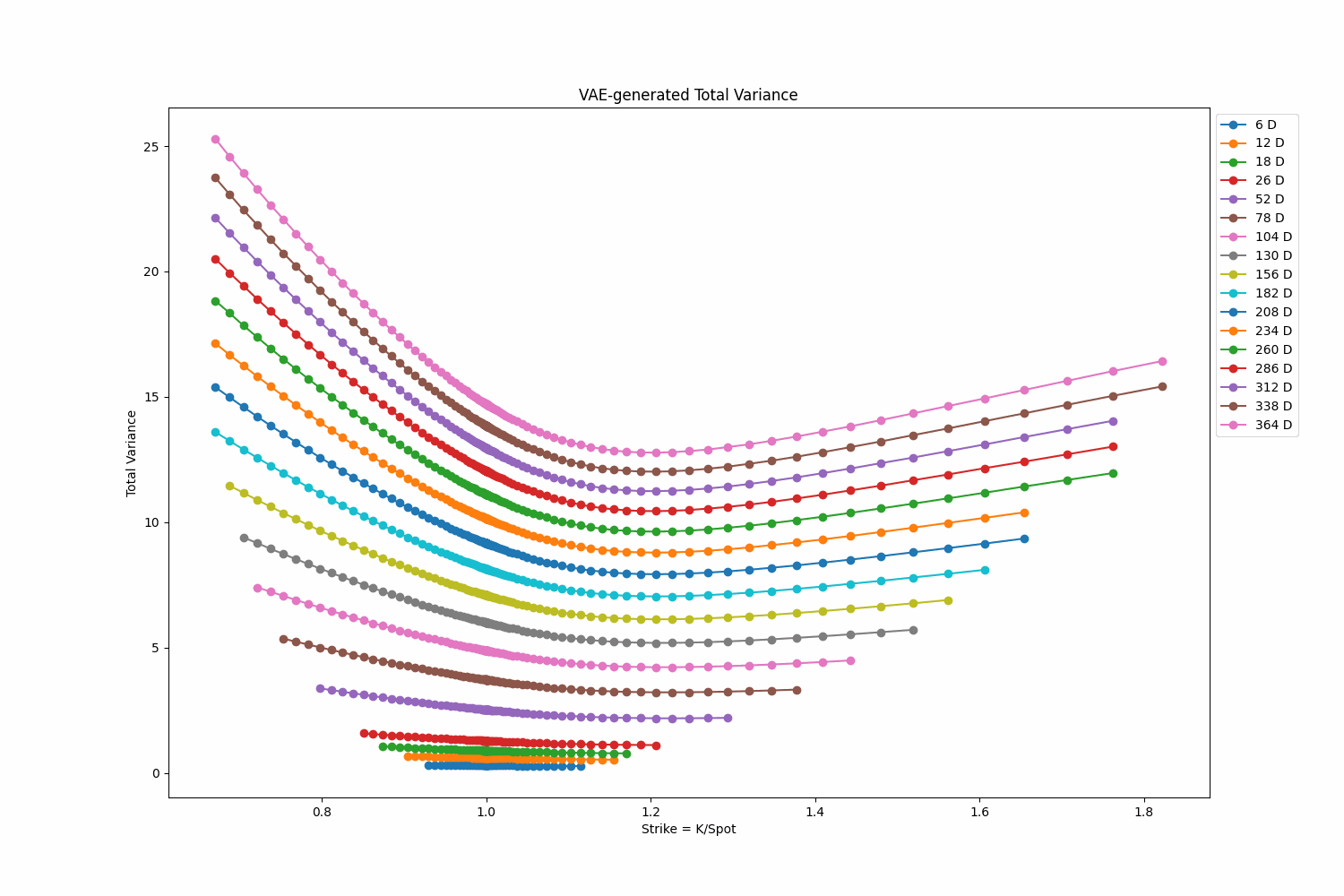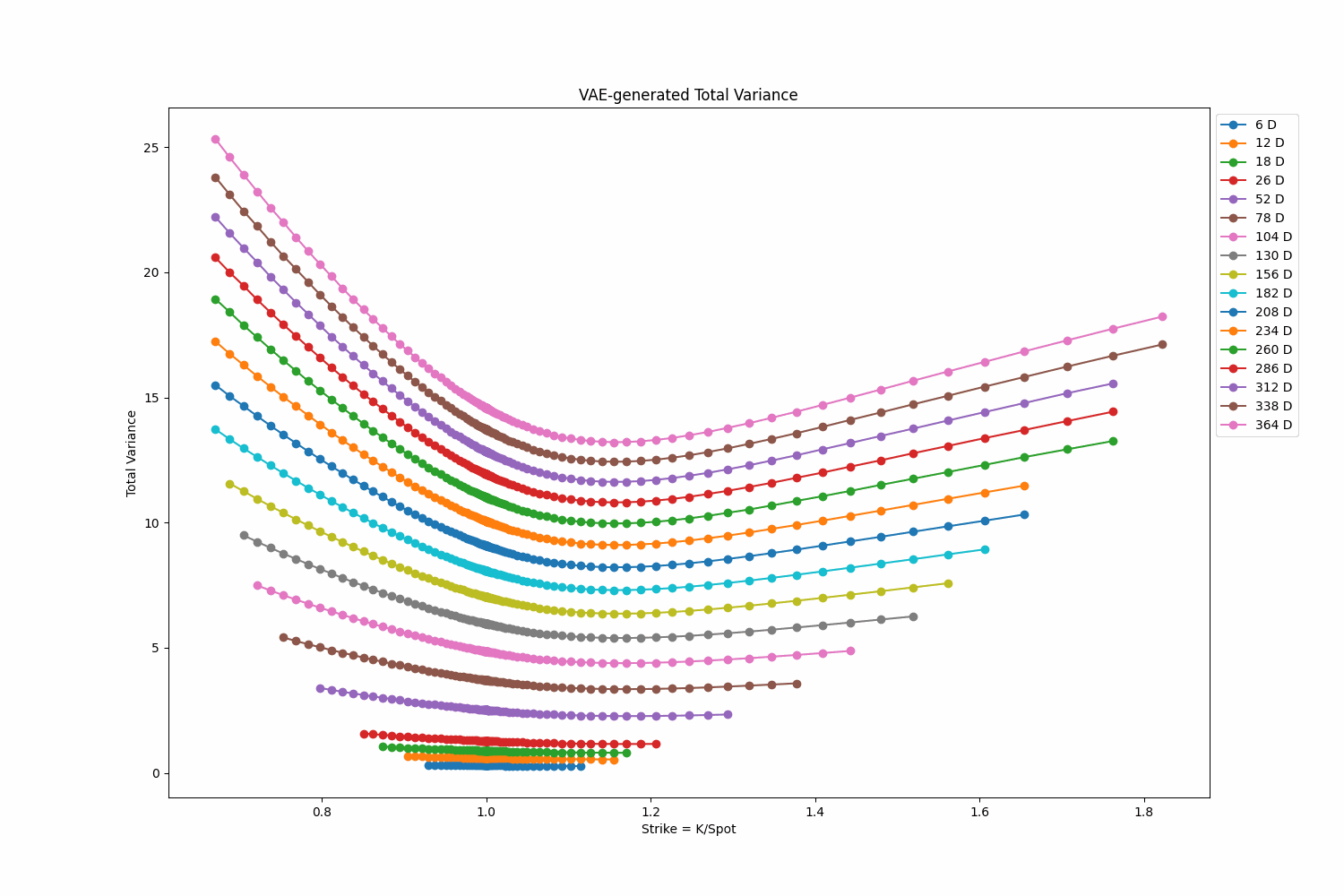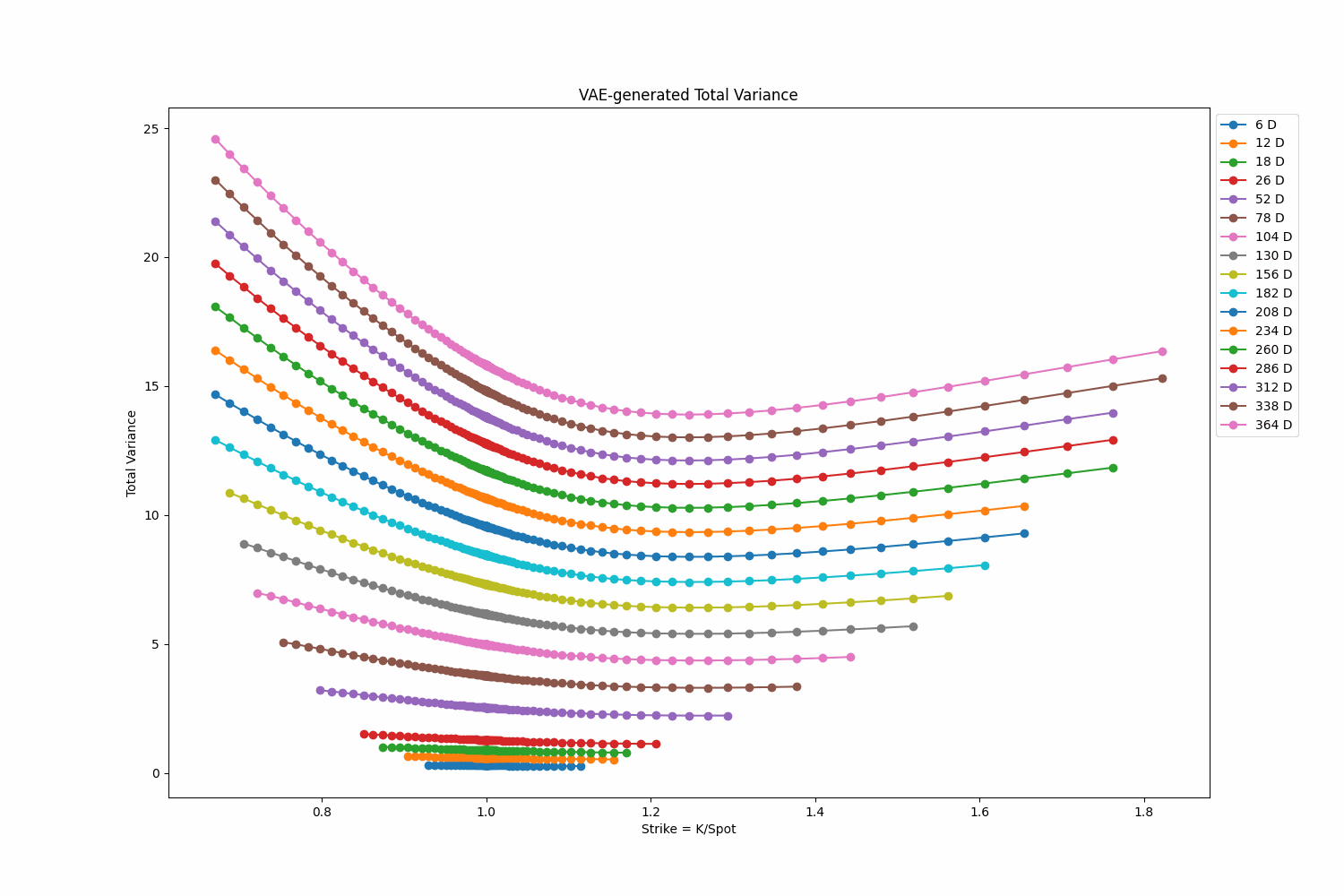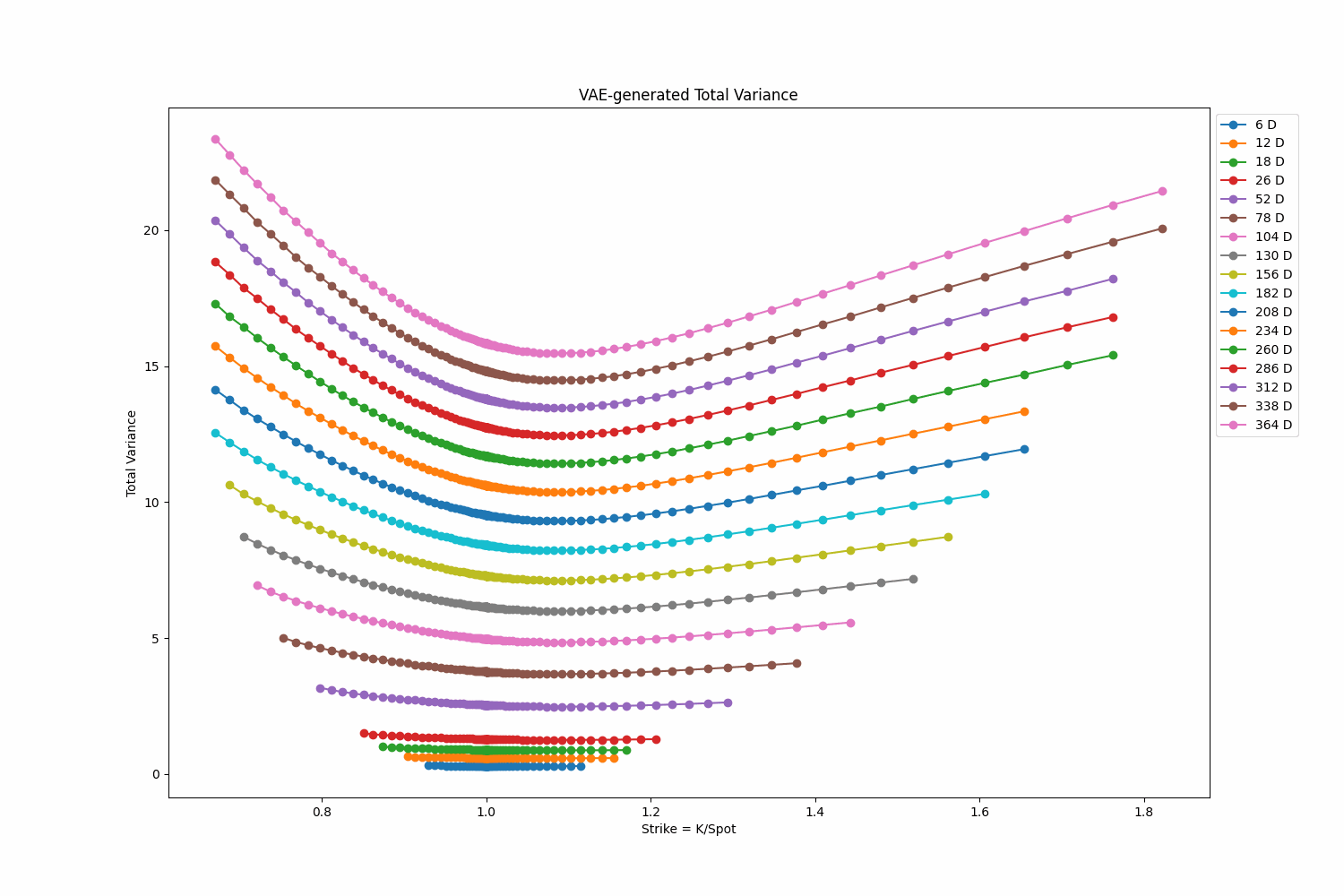
Tags: Variational Autoencoder, Pytorch, Generative AI, Deep Learning, Heston, Volatility Surfaces, Vectorization, Monte Carlo Simulation
Implementing Deep Smoothing for Implied Volatility Surfaces
This project is a python-based implementation of the methodologies presented in the paper Deep Smoothing of the Implied Volatility Surface with different aspects related to the neural network training, convergence behavior, and associated implementation details developed independently.
A volatility surface is a representation of implied volatility across different strike prices and maturities, crucial for pricing and hedging options accurately. Ensuring the surface is arbitrage-free is essential to prevent inconsistencies that could lead to riskless profit opportunities, which would undermine the model’s reliability in real markets. Deep smoothing focuses on applying deep learning methods to generate smooth, arbitrage-free implied volatility surfaces which at a high-level can be summarized as follows: Imagine you are given a set of points \((k, \tau, iv)\) representing market data. These points form part of a 3D surface that we aim to construct with two key objectives:
- We need to fit the market data.
- We must ensure that the surface meets certain curvature properties. In quantitative finance, this means creating an arbitrage-free surface. Mathematically, this translates to minimizing a specified loss function across the entire surface.
To see project’s page, click here. You can find the code for this project here.
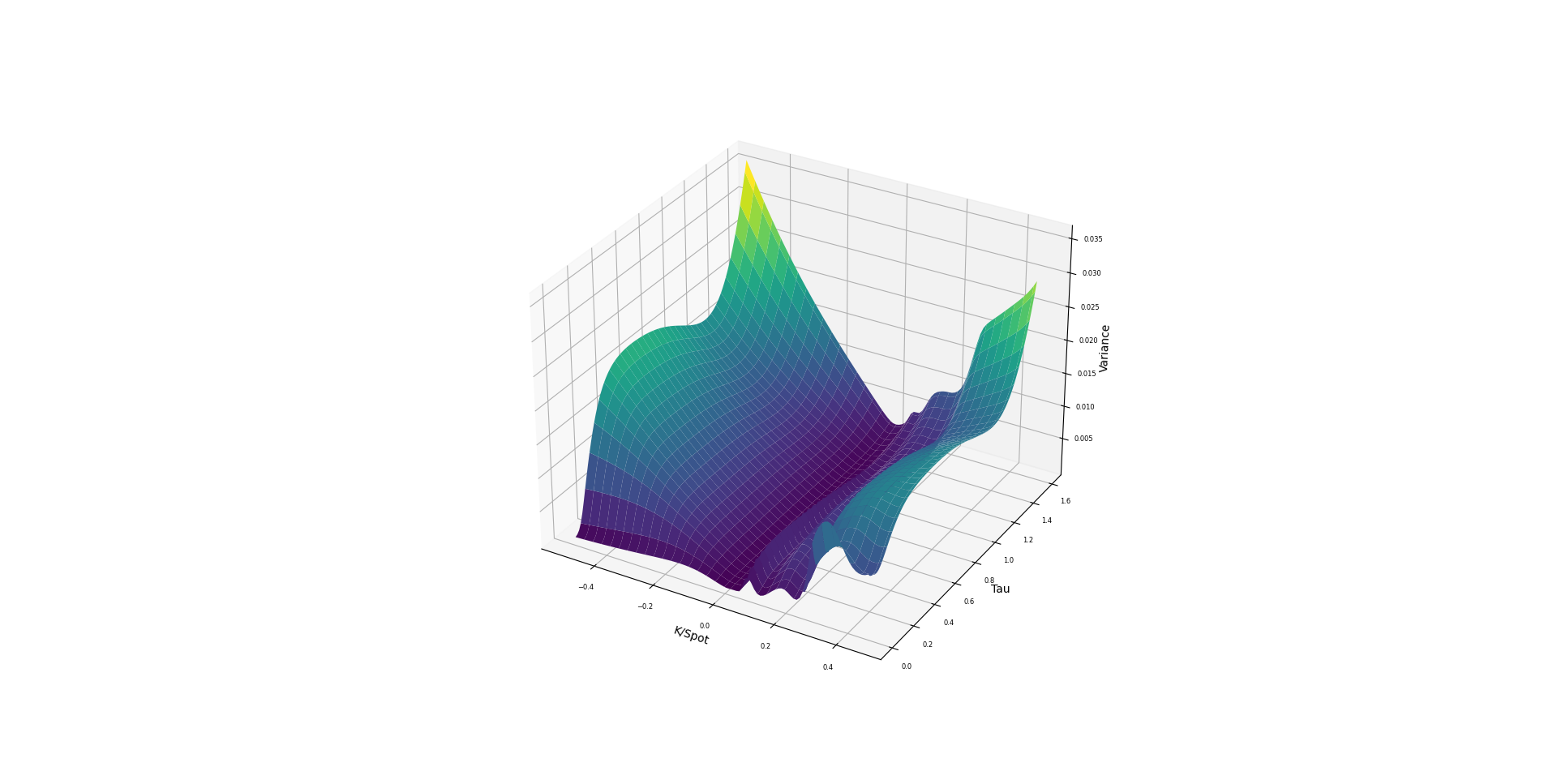
Tags: Deep Learning, Pytorch, Feed Forward Networks, Volatility Surfaces, Vectorization, SSVI, Convex Optimization, CVX
Quantitative Finance and Option Pricing
Once upon a time, I became interested in quantitaive finance, in particular Option Pricing. Stochastic models are used for option pricing where the underlying uncertainly is driven by a class of continous time martingales known as Wiener processes. The classic source for learning about options and how they are priced is Stochastic Calculus for Finance II written by Shreve. I typed up my own solutions to all of this book’s exercises and you could find them here.
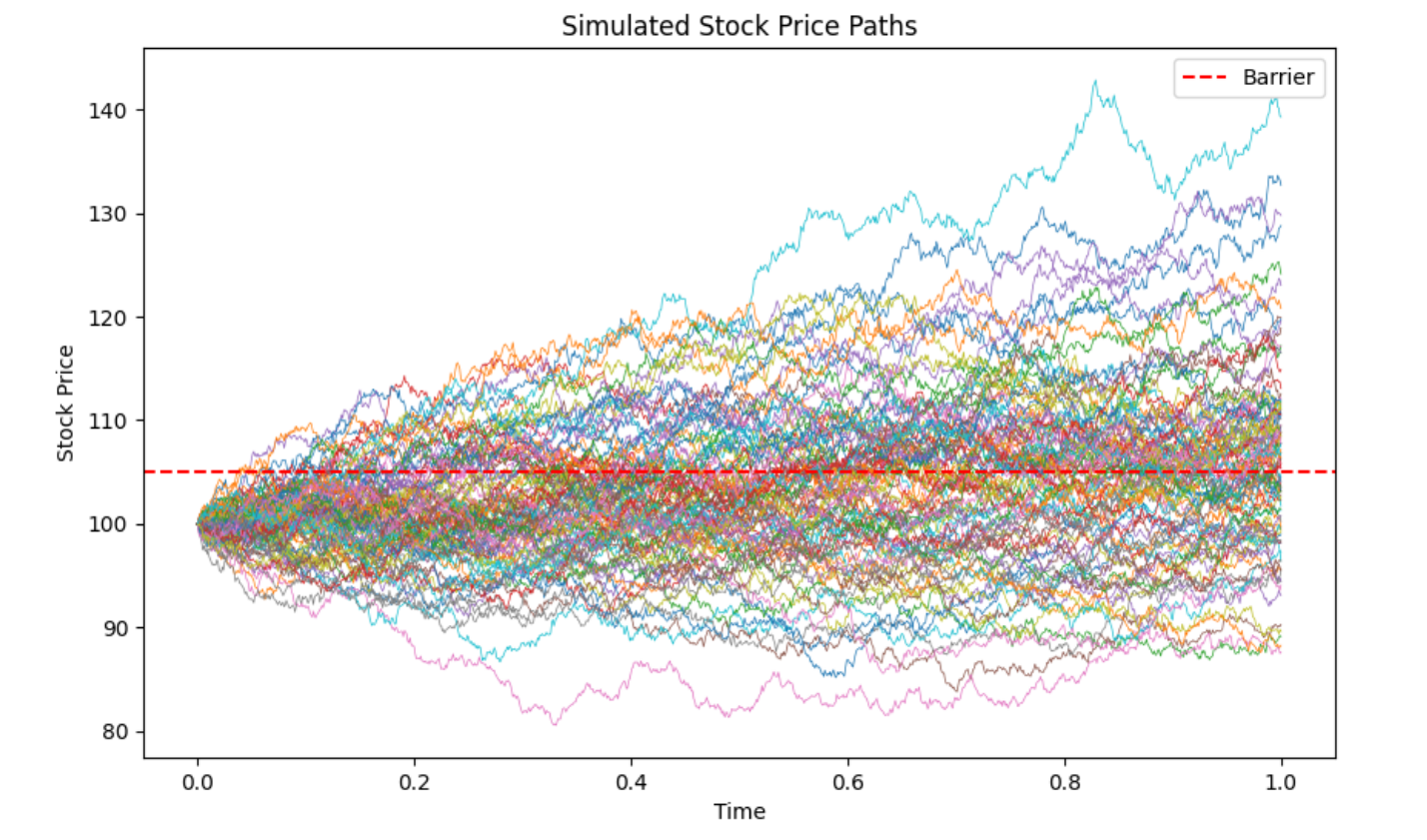
A Termination Criterion for Stochastic Gradient Descent for Binary Classification
Early stopping rules and termination criteria play a central role in machine learning. Models trained via first order methods without early stopping may not predict well on future data since they over-fit the given samples. For my PhD project, I worked on a simple and computationally inexpensive termination criterion which exhibits a good degree of predictability on yet unseen data. Theoretical and numerical evidence are also provided for the effectiveness of the test. I presented the results at OPT2020 (Workshop on Optimization for Machine Learning with Neurips). To see the poster, click here.

Tags: Stochastic Gradient Descent, Logistic Regression, Mixure of Gaussians, Binary Classification, Early Stopping, Overtfitting, Markov Chains, Stochastic Stability
